Probabilities, odds, odds ratios

Prof. Maria Tackett

Mar 24, 2025

Announcements

  • Project Presentations in lab on Friday, March 28

  • Lab 06 due TODAY at 11:59pm

  • Statistics experience due April 22


Drop-in Peer Advising will be happening Wednesday, March 26, from 6:30-8:30 PM in Bostock Lounge for students to stop by with any questions they have around STA/CS/MATH classes, major pathways, or other general advice since shopping carts just opened. 

Fall 2025 STA classes

  • STA 240: Probability for Statistical Inference, Modeling, and Data Analysis (or STA 230 or STA 231)

  • STA 322: Study Design: Design of Surveys and Causal Studies

  • STA 323: Statistical Computing

  • STA 325: Machine Learning and Data Mining (need STA 230/231/240)

  • STA 332: Statistical Inference (need STA 230/231/240)

  • STA 344: Introduction to Statistical Modeling of Spatial and Time Series data (need STA 230/231/240)

  • STA 402: Bayesian Statistical Modeling and Data Analysis (need STA 332)

  • STA 465: Introduction to High Dimensional Data Analysis

Topics

  • Review: Multicollinearity vs. interaction effects

  • Logistic regression for binary response variable

  • Relationship between odds and probabilities

  • Odds ratios

Computational setup

# load packages
library(tidyverse)
library(tidymodels)
library(knitr)
library(patchwork)
library(Stat2Data) #contains sleep data set

# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Review: Multicollinearity vs. interactions

Suppose we fit a model using flipper length and bill length to understand variability in body mass for Palmer Penguins. We make the plots below as part of the EDA.

What are we checking in Plot 1? In Plot 2?

Predicting categorical outcomes

Types of outcome variables

Quantitative outcome variable:

  • Sales price of a house in Duke Forest
  • Model: Expected sales price given the number of bedrooms, lot size, etc.

Categorical outcome variable:

  • Indicator of being high risk of getting coronary heart disease in the next 10 years
  • Model: Probability an adult is high risk of heart disease in the next 10 years given their age, total cholesterol, etc.

Models for categorical outcomes

Logistic regression

2 Outcomes

1: Yes, 0: No

Multinomial logistic regression

3+ Outcomes

1: Democrat, 2: Republican, 3: Independent

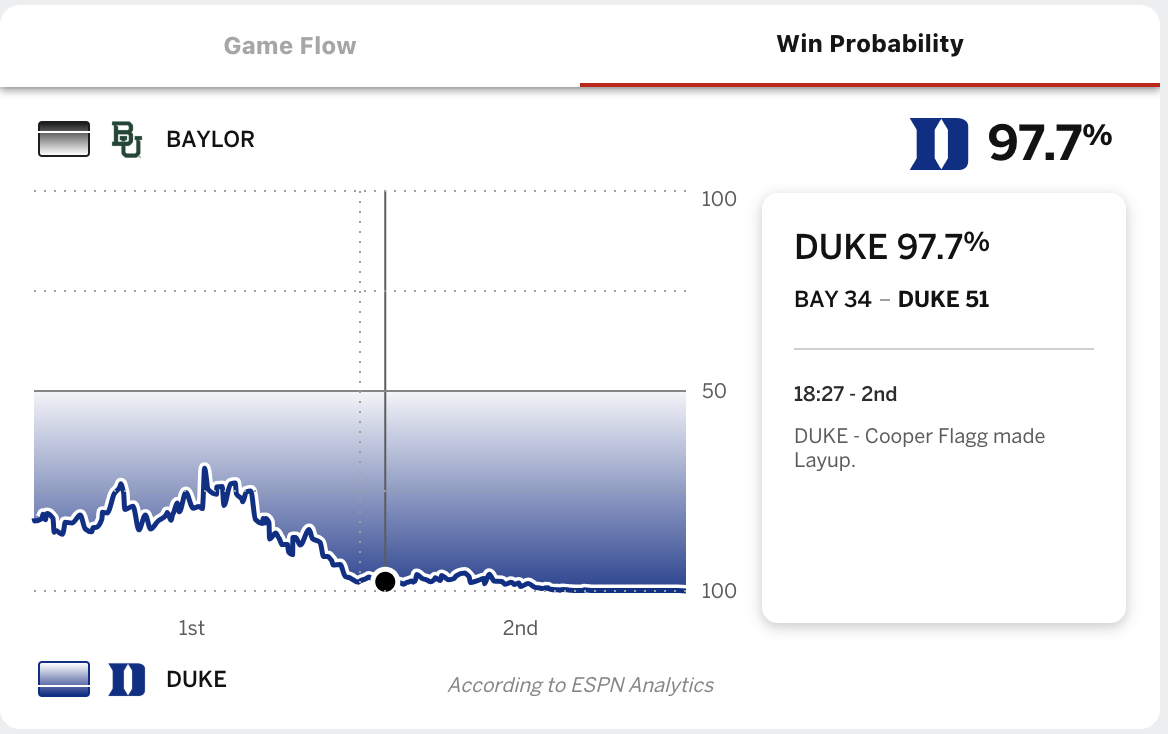
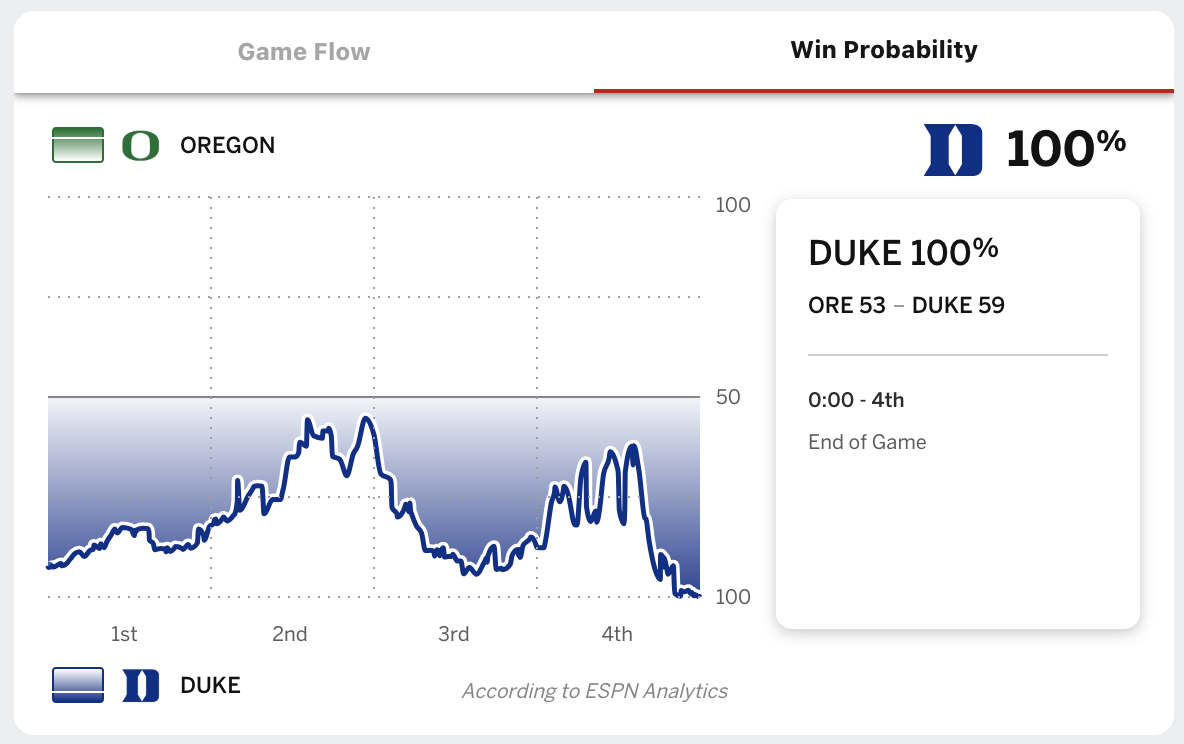
Example: Win probabilities

Duke in 2nd round of NCCA March Madness Tournaments


Men’s Basketball

Source: ESPN Gamecast
Women’s Basketball

Source: ESPN Gamecast

Do teenagers get 7+ hours of sleep?

Students in grades 9 - 12 were surveyed about health risk behaviors including whether they usually get 7 or more hours of sleep.

Sleep7

1: yes

0: no

# A tibble: 446 × 2
     Age Sleep7
   <int>  <int>
 1    16      1
 2    17      0
 3    18      0
 4    17      1
 5    15      0
 6    17      0
 7    17      1
 8    16      1
 9    16      1
10    18      0
# ℹ 436 more rows

Plot the data

ggplot(sleep, aes(x = Age, y = Sleep7)) +
  geom_point() + 
  labs(y = "Getting 7+ hours of sleep")

Let’s fit a linear regression model

Outcome: Y = 1: yes, 0: no

Let’s use proportions

Outcome: Probability of getting 7+ hours of sleep

What happens if we zoom out?

Outcome: Probability of getting 7+ hours of sleep

🛑 This model produces predictions outside of 0 and 1.

Let’s try another model

✅ This model (called a logistic regression model) only produces predictions between 0 and 1.

The code

ggplot(sleep_age, aes(x = Age, y = prop)) +
  geom_point() + 
  geom_hline(yintercept = c(0,1), lty = 2) + 
  stat_smooth(method ="glm", method.args = list(family = "binomial"), 
              fullrange = TRUE, se = FALSE) +
  labs(y = "P(7+ hours of sleep)") +
  xlim(1, 40) +
  ylim(-0.5, 1.5)

Different types of models

Method Outcome Model
Linear regression Quantitative y=Xβ+ϵ
Linear regression (transform Y) Quantitative log⁡(y)=Xβ+ϵ
Logistic regression Binary log⁡(π1−π)=Xβ

Linear vs. logistic regression

State whether a linear regression model or logistic regression model is more appropriate for each scenario.

  1. Use age and political party to predict if a randomly selected person will vote in the next election.

  2. Use budget and run time (in minutes) to predict a movie’s total revenue.

  3. Use age and sex to calculate the probability a randomly selected adult will visit Duke Health in the next year.

Probabilities and odds

Data: Concern about rising AI

This data comes from the 2023 Pew Research Center’s American Trends Panel. The survey aims to capture public opinion about a variety of topics including politics, religion, and technology, among others. We will use data from 11201 respondents in Wave 132 of the survey conducted July 31 - August 6, 2023.


The goal of this analysis is to understand the relationship between age, how much someone has heard about artificial intelligence (AI), and concern about the increased use of AI in daily life.


A more complete analysis on this topic can be found in the Pew Research Center article Growing public concern about the role of artificial intelligence in daily life by Alec Tyson and Emma Kikuchi.

Variables

  • ai_concern: Whether a respondent said they are “more concerned than excited” about in the increased use of AI in daily life (1: yes, 0: no)

Source: Pew Research

Variables

  • ai_heard : Response to the question “How much have you heard or read about AI?”

    • A lot
    • A little
    • Nothing at all
    • Refused

  • age_cat: Age category

    • 18-29
    • 30-49
    • 50-64
    • 65+
    • Refused

Data prep

# change variable names and recode categories
pew_data <- pew_data |>
  mutate(ai_concern = if_else(CNCEXC_W132 == 2, 1, 0),
         age_cat = case_when(F_AGECAT == 1 ~ "18-29",
                             F_AGECAT == 2 ~ "30-49",
                             F_AGECAT == 3 ~ "50-64",
                             F_AGECAT == 4 ~ "65+",
                             TRUE ~ "Refused"), 
         ai_heard = case_when(AI_HEARD_W132 == 1 ~ "A lot",
                              AI_HEARD_W132 == 2 ~ "A little",
                              AI_HEARD_W132 == 3 ~ "Nothing at all",
                              TRUE ~ "Refused"
                              ))

# Make factors and  relevel 
pew_data <- pew_data |>
  mutate(ai_concern = factor(ai_concern),
         age_cat = factor(age_cat), 
         ai_heard = factor(ai_heard, levels = c("A lot", "A little", "Nothing at all", "Refused"))
  )

Univariate EDA

Binary response variable

  • Y=1: yes (success), 0: no (failure)

  • π: probability that Y=1, i.e., P(Y=1)

  • π1−π: odds that Y=1

  • log⁡(π1−π): log odds

  • Go from π to log⁡(π1−π) using the logit transformation

Example

Suppose there is a 70% chance it will rain tomorrow

  • Probability it will rain is π=0.7
  • Probability it won’t rain is 1−π=0.3
  • Odds it will rain are 7 to 3, 7:3, 0.70.3≈2.33

Concerned about AI in daily life?

pew_data |>
  count(ai_concern) |>
  mutate(pi = round(n / sum(n), 3))
# A tibble: 2 × 3
  ai_concern     n    pi
  <fct>      <int> <dbl>
1 0           5245 0.468
2 1           5956 0.532


P(Concerned about AI)=P(Y=1)=π=0.532

P(Not concerned about AI)=P(Y=0)=1−π=0.468

Odds of being concerned about AI=0.5320.468=1.137

From odds to probabilities

odds

odds=π1−π

probability

π=odds1+odds

Odds ratios

Concern about AI vs. age

Age Not Concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

Compare the odds for two groups

Age Not Concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

We want to compare concern about increased use of AI in daily life between individuals who are 18-29 years old to those who are 65+ years old

Compare the odds for two groups

Age Not Concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

We’ll use the odds to compare the two groups

odds=P(success)P(failure)=# of successes# of failures

Compare the odds for two groups

Age Not Concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

  • Odds of being concerned with increased use of AI in daily life for 18-29 year olds: 416550=0.756

  • Odds of being concerned with increased use of AI in daily life for those who are 65+ years old: 20131376=1.463

  • Based on this, we see that individuals 65+ years old are more likely to be concerned about the increased use of AI in daily life than 18-29 year olds.

Odds ratio (OR)

Age Not Concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

Let’s summarize the relationship between the two groups. To do so, we’ll use the odds ratio (OR).

OR=odds1odds2

OR: AI concern by age

Age Not Concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

OR=odds18−29odds65+=0.7561.463=0.517

The odds an 18-29 year old is concerned about increased use of AI in daily life are 0.517 times the odds a 65+ year old is concerned.

More natural interpretation

  • It’s more natural to interpret the odds ratio with a statement with the odds ratio greater than 1.

  • The odds a 65+ year old is concerned about increased use of AI in daily life are 1.934 (1/0.517) times the odds an 18-29 year old is concerned.

Code to make table

pew_data |>
  count(age_cat, ai_concern)
# A tibble: 10 × 3
   age_cat ai_concern     n
   <fct>   <fct>      <int>
 1 18-29   0            550
 2 18-29   1            416
 3 30-49   0           1898
 4 30-49   1           1681
 5 50-64   0           1398
 6 50-64   1           1818
 7 65+     0           1376
 8 65+     1           2013
 9 Refused 0             23
10 Refused 1             28

Code to make table

pew_data |>
  count(age_cat, ai_concern) |>
  pivot_wider(names_from = ai_concern, values_from = n)
# A tibble: 5 × 3
  age_cat   `0`   `1`
  <fct>   <int> <int>
1 18-29     550   416
2 30-49    1898  1681
3 50-64    1398  1818
4 65+      1376  2013
5 Refused    23    28

Code to make table

pew_data |>
  count(age_cat, ai_concern) |>
  pivot_wider(names_from = ai_concern, values_from = n) |>
  kable()
age_cat 0 1
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

Code to make table

pew_data |>
  count(age_cat, ai_concern) |>
  pivot_wider(names_from = ai_concern, values_from = n) |>
  kable(col.names = c("Age", "Not concerned", "Concerned"))
Age Not concerned Concerned
18-29 550 416
30-49 1898 1681
50-64 1398 1818
65+ 1376 2013
Refused 23 28

Application exercise

📋 sta221-sp25.netlify.app/ae/ae-05-prob-odds.html

Recap

  • Introduced logistic regression for binary response variable

  • Showed the relationship between odds and probabilities

  • Introduced odds ratios

🔗 STA 221 - Spring 2025

1 / 43
Probabilities, odds, odds ratios Prof. Maria Tackett Mar 24, 2025

  1. Slides

  2. Tools

  3. Close
  • Probabilities, odds, odds ratios
  • Announcements
  • Fall 2025 STA classes
  • Topics
  • Computational setup
  • Review: Multicollinearity vs. interactions
  • Predicting categorical outcomes
  • Types of outcome variables
  • Models for categorical outcomes
  • Example: Win probabilities
  • Do teenagers get 7+ hours of sleep?
  • Plot the data
  • Let’s fit a linear regression model
  • Let’s use proportions
  • What happens if we zoom out?
  • Let’s try another model
  • The code
  • Different types of models
  • Linear vs. logistic regression
  • Probabilities and odds
  • Data: Concern about rising AI
  • Variables
  • Variables
  • Data prep
  • Univariate EDA
  • Binary response variable
  • Example
  • Concerned about AI in daily life?
  • From odds to probabilities
  • Odds ratios
  • Concern about AI vs. age
  • Compare the odds for two groups
  • Compare the odds for two groups
  • Compare the odds for two groups
  • Odds ratio (OR)
  • OR: AI concern by age
  • More natural interpretation
  • Code to make table
  • Code to make table
  • Code to make table
  • Code to make table
  • Application exercise
  • Recap
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • r Scroll View Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help