Multiple linear regression (MLR)

Topics

• Introducing multiple linear regression

  • Exploratory data analysis for multiple linear regression

  • Fitting the least squares line

  • Interpreting coefficients for quantitative predictors

  • Prediction

Computing setup

# load packages
library(tidyverse)
library(tidymodels)
library(openintro)
library(patchwork)
library(knitr)
library(kableExtra)

# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_minimal(base_size = 16))

Data: Peer-to-peer lender

Today’s data is a sample of 50 loans made through a peer-to-peer lending club. The data is in the loan50 data frame in the openintro R package.

# A tibble: 50 × 4
   annual_income debt_to_income verified_income interest_rate
           <dbl>          <dbl> <fct>                   <dbl>
 1         59000         0.558  Not Verified            10.9 
 2         60000         1.31   Not Verified             9.92
 3         75000         1.06   Verified                26.3 
 4         75000         0.574  Not Verified             9.92
 5        254000         0.238  Not Verified             9.43
 6         67000         1.08   Source Verified          9.92
 7         28800         0.0997 Source Verified         17.1 
 8         80000         0.351  Not Verified             6.08
 9         34000         0.698  Not Verified             7.97
10         80000         0.167  Source Verified         12.6 
# ℹ 40 more rows

Variables

Predictors:

• annual_income: Annual income
• debt_to_income: Debt-to-income ratio, i.e. the percentage of a borrower’s total debt divided by their total income
• verified_income: Whether borrower’s income source and amount have been verified (Not Verified, Source Verified, Verified)

Outcome: interest_rate: Interest rate for the loan

Outcome: interest_rate

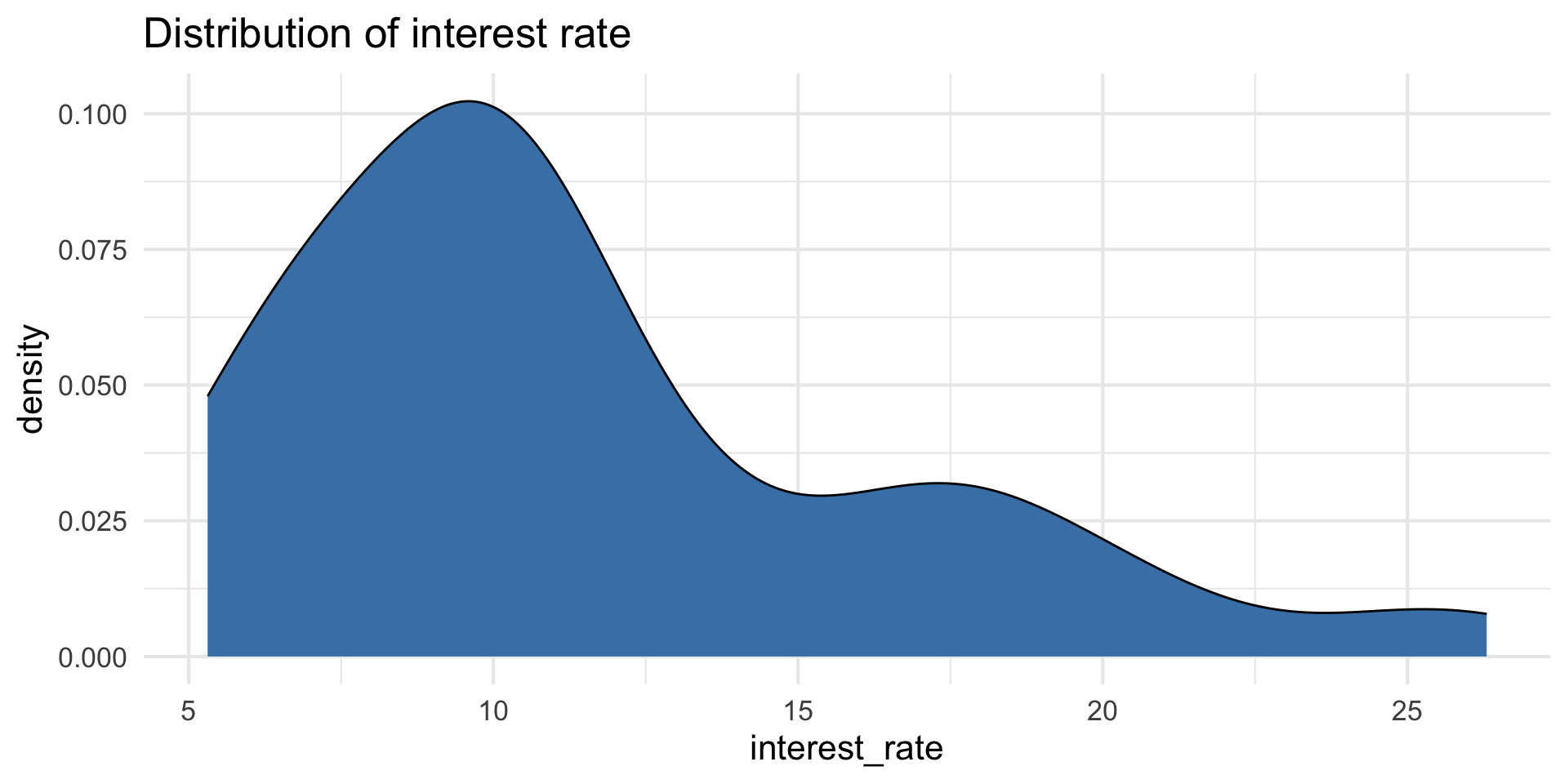
Min	Median	Max	IQR
5.31	9.93	26.3	5.755

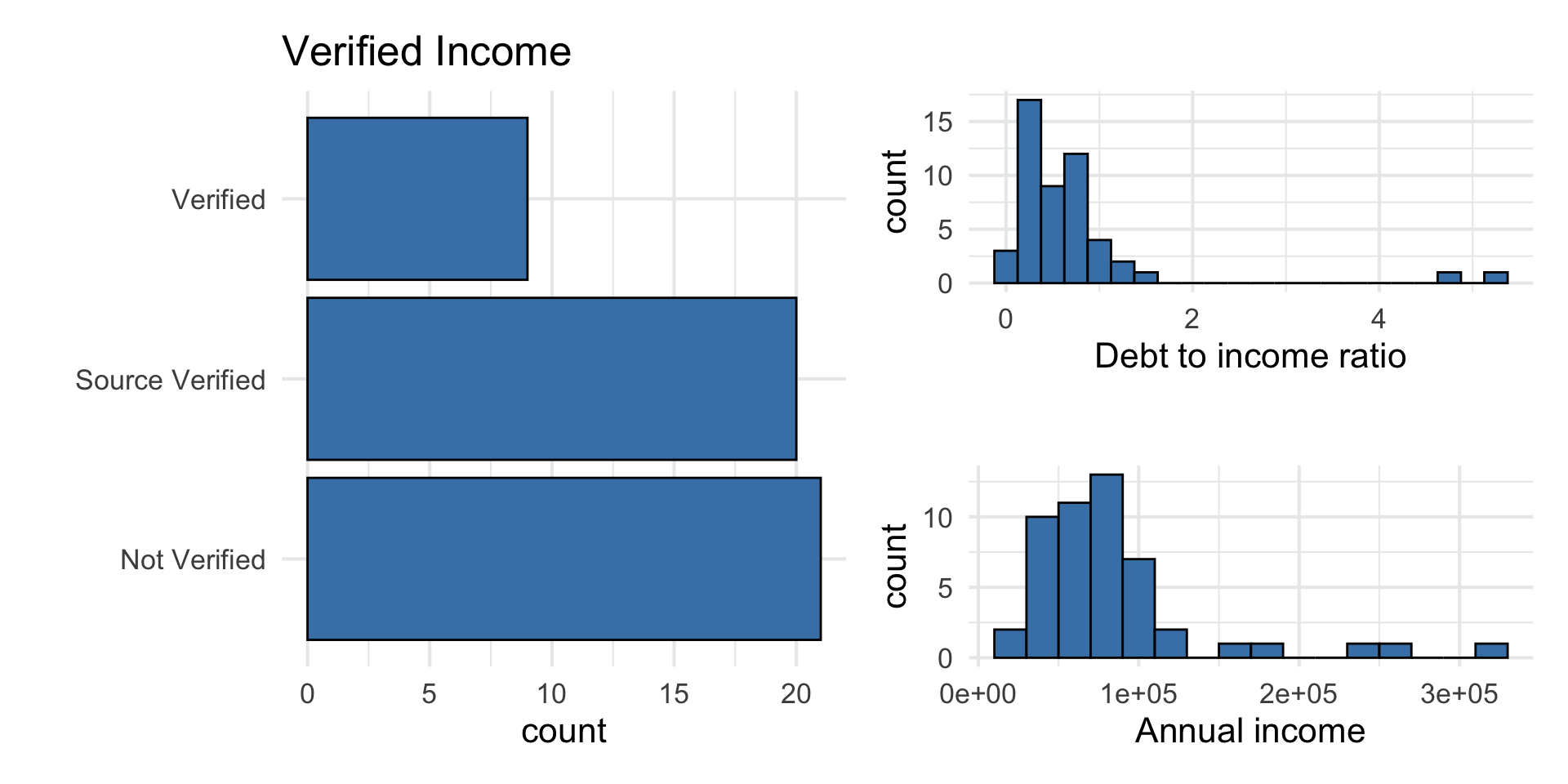
Predictors

Data manipulation 1: Rescale income

loan50 <- loan50 |>
  mutate(annual_income_th = annual_income / 1000)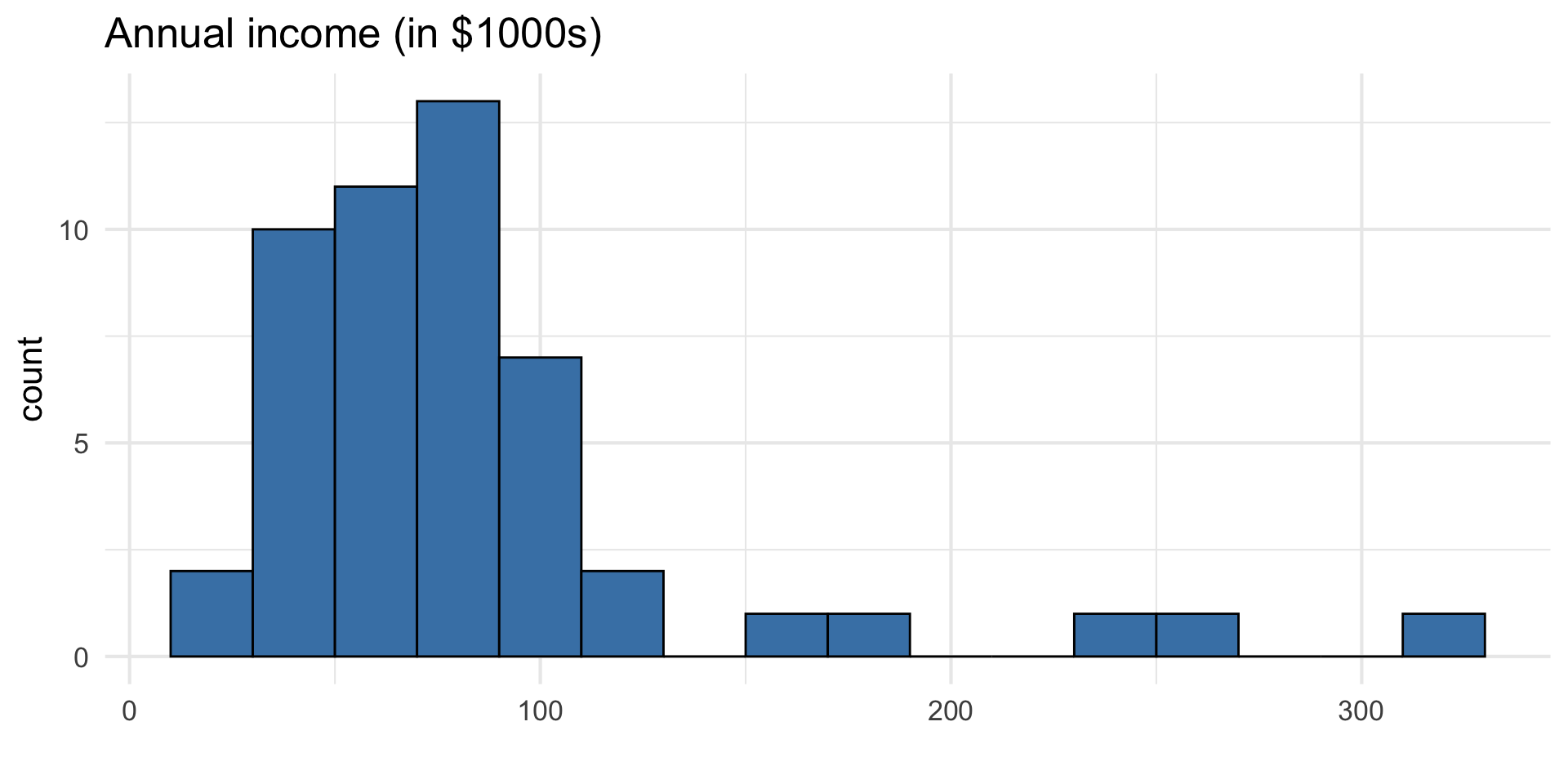

. . .

Why did we rescale income?

Outcome vs. predictors

. . .

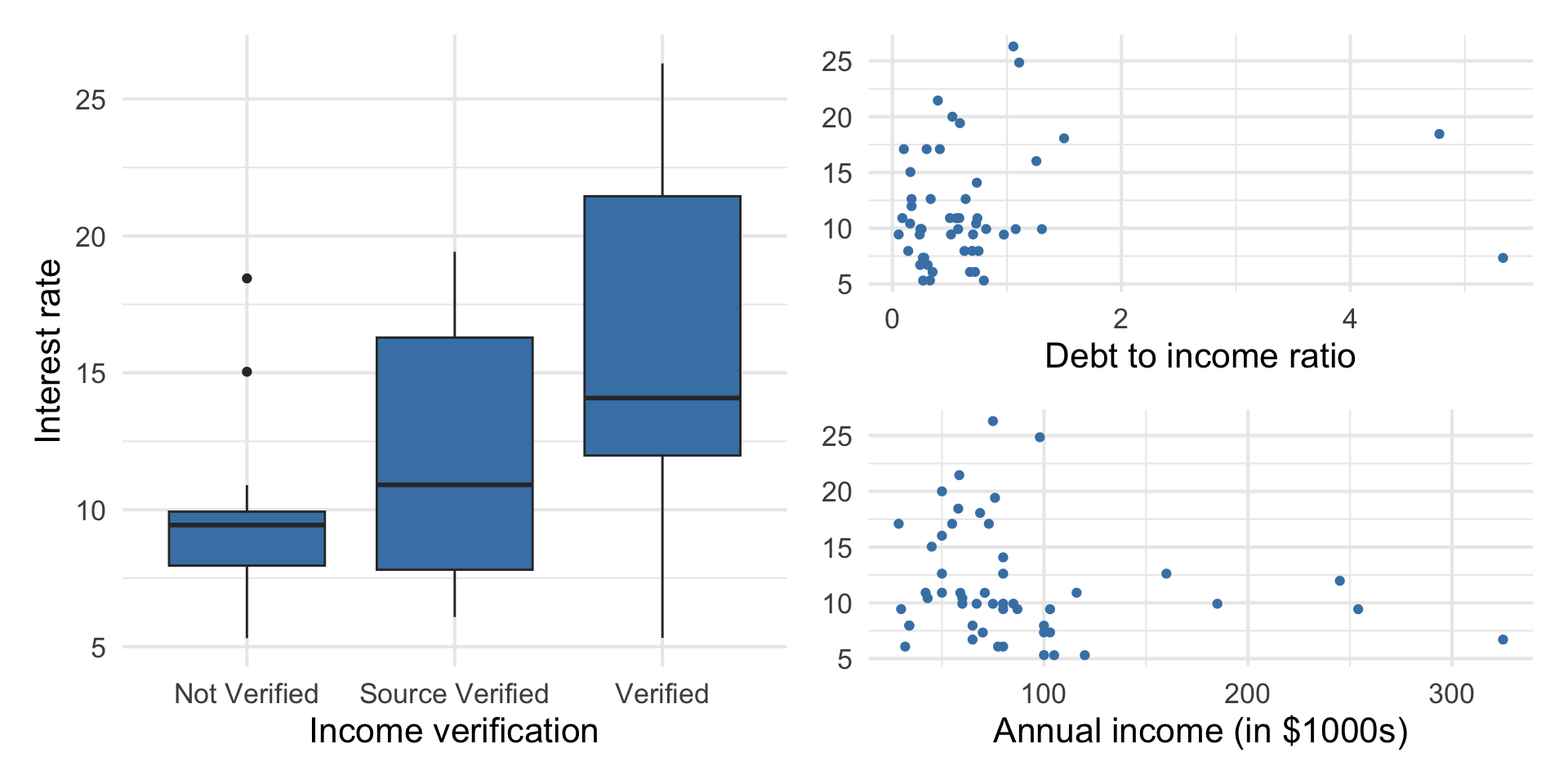
Goal: Use these predictors in a single model to understand variability in interest rate.

. . .

Why do we want to use a single model versus 3 separate simple linear regression models?

Multiple linear regression (MLR)

Multiple linear regression (MLR)

Based on the analysis goals, we will use a multiple linear regression model of the following form

$$\begin{array}{rl}\text{interest\_rate}={\beta }_0& +{\beta }_1\text{debt\_to\_income}\\ & +{\beta }_2\text{verified\_income}\\ & +{\beta }_3\text{annual\_income\_th}\\ & +ϵ,ϵ\sim N(0,{\sigma }_{ϵ}^2)\end{array}$$

Multiple linear regression

Recall: The simple linear regression model

$$Y={\beta }_0+{\beta }_{1}X+ϵ$$

. . .

The form of the multiple linear regression model is

$$Y={\beta }_0+{\beta }_1{X}_1+\cdots +{\beta }_p{X}_p+ϵ$$

. . .

Therefore,

$$E(Y|X_1,\dots ,X_p)={\beta }_0+{\beta }_1{X}_1+\cdots +{\beta }_p{X}_p$$

Fitting the least squares line

Similar to simple linear regression, we want to find estimates for ${\beta }_0,{\beta }_1,\dots ,{\beta }_p$ that minimize

$$\sum _{i=1}^n{ϵ}_i^2=\sum _{i=1}^n[y_i-{\hat{y}}_i{]}^2=\sum _{i=1}^n[y_i-({\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}){]}^2$$

. . .

The calculations can be very tedious, especially if $p$ is large

Matrix form of multiple linear regression

Suppose we have $n$ observations, a quantitative response variable, and $p$ > 1 predictors $$\underset{\mathbf{y}}{\underbrace{\left[\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right]}}=\underset{\mathbf{X}}{\underbrace{\left[\begin{array}{cccc}1& x_{11}& \dots & x_{1p}\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_{n1}& \dots & x_{np}\end{array}\right]}}\underset{\mathit{\beta }}{\underbrace{\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right]}}+\underset{\mathit{ϵ}}{\underbrace{\left[\begin{array}{c}{ϵ}_1\\ ⋮\\ {ϵ}_n\end{array}\right]}}$$

What are the dimensions of $\mathbf{y}$, $\mathbf{X}$, $\mathit{\beta }$, $\mathit{ϵ}$?

Matrix form of multiple linear regression

As with simple linear regression, we have

$$\mathbf{Y}=\mathbf{X}\mathit{\beta }+\mathit{ϵ}$$

. . .

Generalizing the derivations from SLR to $p>2$, we have

$$\hat{\mathit{\beta }}=({\mathbf{X}}^{\mathsf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathsf{T}}\mathbf{y}$$

as before.

Model fit in R

int_fit <- lm(interest_rate ~ debt_to_income + verified_income  + annual_income_th,
              data = loan50)

tidy(int_fit) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	10.726	1.507	7.116	0.000
debt_to_income	0.671	0.676	0.993	0.326
verified_incomeSource Verified	2.211	1.399	1.581	0.121
verified_incomeVerified	6.880	1.801	3.820	0.000
annual_income_th	-0.021	0.011	-1.804	0.078

Model equation

$$\begin{array}{rl}\widehat{\text{interest\_rate}}=10.726& +0.671\times \text{debt\_to\_income}\\ & +2.211\times \text{source\_verified}\\ & +6.880\times \text{verified}\\ & -0.021\times \text{annual\_income\_th}\end{array}$$

Note

We will talk about why there are only two terms in the model for verified_income soon!

Interpreting ${\hat{\beta }}_j$

• The estimated coefficient ${\hat{\beta }}_j$ is the expected change in the mean of $Y$ when $X_j$ increases by one unit, holding the values of all other predictor variables constant.

. . .

• Example: The estimated coefficient for debt_to_income is 0.671. This means for each point in an borrower’s debt to income ratio, the interest rate on the loan is expected to be greater by 0.671%, on average, holding annual income and income verification constant.

Interpreting ${\hat{\beta }}_j$

The estimated coefficient for annual_income_th is -0.021. Interpret this coefficient in the context of the data.

Why do we need to include a statement about holding all other predictors constant?

Interpreting ${\hat{\beta }}_0$

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	10.726	1.507	7.116	0.000	7.690	13.762
debt_to_income	0.671	0.676	0.993	0.326	-0.690	2.033
verified_incomeSource Verified	2.211	1.399	1.581	0.121	-0.606	5.028
verified_incomeVerified	6.880	1.801	3.820	0.000	3.253	10.508
annual_income_th	-0.021	0.011	-1.804	0.078	-0.043	0.002

. . .

Describe the subset of borrowers who are expected to get an interest rate of 10.726% based on our model. Is this interpretation meaningful? Why or why not?

Prediction

What is the predicted interest rate for an borrower with an debt-to-income ratio of 0.558, whose income is not verified, and who has an annual income of $59,000?

10.726 + 0.671 * 0.558 + 2.211 * 0 + 6.880 * 0 - 0.021 * 59

[1] 9.861418

. . .

The predicted interest rate for an borrower with with an debt-to-income ratio of 0.558, whose income is not verified, and who has an annual income of $59,000 is 9.86%.

Prediction in R

Just like with simple linear regression, we can use the predict() function in R to calculate the appropriate intervals for our predicted values:

new_borrower <- tibble(
  debt_to_income  = 0.558, 
  verified_income = "Not Verified", 
  annual_income_th = 59
)

predict(int_fit, new_borrower)

       1 
9.890888 

Note

Difference in predicted value due to rounding the coefficients on the previous slide.

Cautions

• Do not extrapolate! Because there are multiple predictor variables, there is the potential to extrapolate in many directions
• The multiple regression model only shows association, not causality
  • To show causality, you must have a carefully designed experiment or carefully account for confounding variables in an observational study

Recap

• Showed exploratory data analysis for multiple linear regression

• Used least squares to fit the regression line

• Interpreted the coefficients for quantitative predictors

• Predicted the response for new observations