Logistic Regression: Inference

Announcements

• Lab 07 due TODAY at 11:59pm

• Team Feedback (email from TEAMMATES) due TODAY at 11:59pm (check email)

• HW 04 due April 10 at 11:59pm

• Next project milestone: Draft and peer review in Friday’s lab

• Exam 02 - April 17 (same format as Exam 01)

  • Exam 02 practice + lecture recordings available

• Statistics experience due April 22

Questions from this week’s content?

Topics

• Test of significance for a subset of predictors

• Inference for a single predictor

Computational setup

library(tidyverse)
library(tidymodels)
library(pROC)      
library(knitr)
library(kableExtra)

# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Risk of coronary heart disease

This data set is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to examine the relationship between various health characteristics and the risk of having heart disease.

• high_risk:

  • 1: High risk of having heart disease in next 10 years
  • 0: Not high risk of having heart disease in next 10 years

• age: Age at exam time (in years)

• totChol: Total cholesterol (in mg/dL)

• currentSmoker: 0 = nonsmoker, 1 = smoker

• education: 1 = Some High School, 2 = High School or GED, 3 = Some College or Vocational School, 4 = College

Modeling risk of coronary heart disease

Using age, totChol, and currentSmoker

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-6.673	0.378	-17.647	0.000	-7.423	-5.940
age	0.082	0.006	14.344	0.000	0.071	0.094
totChol	0.002	0.001	1.940	0.052	0.000	0.004
currentSmoker1	0.443	0.094	4.733	0.000	0.260	0.627

Drop-in-deviance test

Drop-in-deviance test

We will use a drop-in-deviance test (Likelihood Ratio Test) to test

• the overall statistical significance of a logistic regression model

• the statistical significance of a subset of coefficients in the model

Deviance

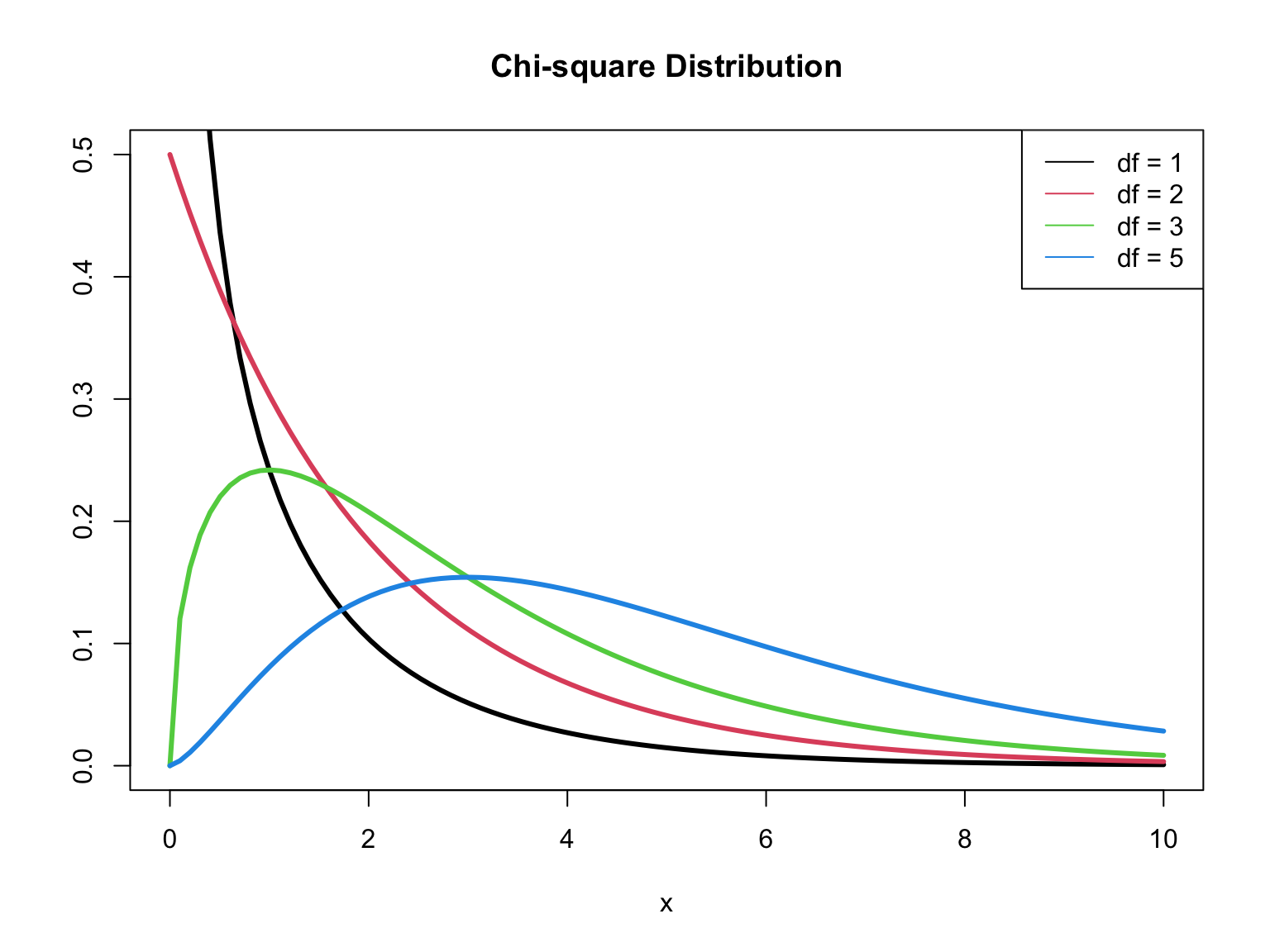
The deviance is a measure of the degree to which the predicted values are different from the observed values (compares the current model to a “saturated” model)

In logistic regression,

$$D=-2\log L$$

$D\sim {\chi }_{n-p-1}^2$ ( $D$ follows a Chi-square distribution with $n-p-1$ degrees of freedom)¹

Note: $n-p-1$ a the degrees of freedom associated with the error in the model (like residuals)

${\chi }^2$ distribution

Test for overall significance

We can test the overall significance for a logistic regression model, i.e., whether there is at least one predictor with a non-zero coefficient

$$\begin{array}{rl}& H_0:{\beta }_1=\cdots ={\beta }_p=0\\ & H_a:{\beta }_j\ne 0\text{ for at least one }j\end{array}$$

. . .

The drop-in-deviance test for overall significance compares the fit of a model with no predictors to the current model.

Drop-in-deviance test statistic

Let $L_0$ and $L_a$ be the likelihood functions of the model under $H_0$ and $H_a$, respectively. The test statistic is

$$\begin{array}{rl}G=D_0-D_a& =(-2\log L_0)-(-2\log L_a)\\ & =-2(\log L_0-\log L_a)\\ & =-2\sum _{i=1}^n[y_i\log (\frac{{\hat{\pi }}^0}{{\hat{\pi }}_i^a})+(1-y_i)\log (\frac{1-{\hat{\pi }}^0}{1-{\hat{\pi }}_i^a})]\end{array}$$

where ${\hat{\pi }}^0$ is the predicted probability under $H_0$ and ${\hat{\pi }}_i^a=\frac{\exp \{x_i^{\mathsf{T}}\mathit{\beta }\}}{1+\exp \{x_i^{\mathsf{T}}\mathit{\beta }\}}$ is the predicted probability under $H_a$

Drop-in-deviance test statistic

$$G=-2\sum _{i=1}^n[y_i\log (\frac{{\hat{\pi }}^0}{{\hat{\pi }}_i^a})+(1-y_i)\log (\frac{1-{\hat{\pi }}^0}{1-{\hat{\pi }}_i^a})]$$

. . .

• When $n$ is large, $G\sim {\chi }_p^2$, ( $G$ follows a Chi-square distribution with $p$ degrees of freedom)²

• The p-value is calculated as $P({\chi }^2>G)$

• Large values of $G$ (small p-values) indicate at least one ${\beta }_j$ is non-zero

Heart disease model: drop-in-deviance test

$$\begin{array}{rl}& H_0:{\beta }_{age}={\beta }_{totChol}={\beta }_{currentSmoker}=0\\ & H_a:{\beta }_j\ne 0\text{ for at least one }j\end{array}$$

. . .

Fit the null model (we’ve already fit the alternative model)

null_model <- glm(high_risk ~ 1, data = heart_disease, family = "binomial")

term	estimate	std.error	statistic	p.value
(Intercept)	-1.72294	0.0436342	-39.486	0

Heart disease model: drop-in-deviance test

Calculate the log-likelihood for the null and alternative models

(L_0 <- glance(null_model)$logLik)

[1] -1737.735

(L_a <- glance(high_risk_fit)$logLik)

[1] -1612.406

. . .

Calculate the likelihood ratio test statistic

(G <- -2 * (L_0 - L_a))

[1] 250.6572

. . .

Heart disease model: likelihood ratio test

Calculate the p-value

(p_value <- pchisq(G, df = 3, lower.tail = FALSE))

[1] 4.717158e-54

. . .

Conclusion

The p-value is small, so we reject $H_0$. The data provide evidence that at least one predictor in the model has a non-zero coefficient.

Why use overall test?

Why do we use a test for overall significance instead of just looking at the test for individual coefficients?³

. . .

Suppose we have a model such that $p=100$ and $H_0:{\beta }_1=\cdots ={\beta }_{100}=0$ is true

. . .

• About 5% of the p-values for individual coefficients will be below 0.05 by chance.

• So we expect to see 5 small p-values if even no linear association actually exists.

• Therefore, it is very likely we will see at least one small p-value by chance.

• The overall test of significance does not have this problem. There is only a 5% chance we will get a p-value below 0.05, if a relationship truly does not exist.

Test a subset of coefficients

Testing a subset of coefficients

• Suppose there are two models:

  • Reduced Model: includes predictors $x_1,\dots ,x_q$

  • Full Model: includes predictors $x_1,\dots ,x_q,x_{q+1},\dots ,x_p$

• We can use a drop-in-deviance test to determine if any of the new predictors are useful

. . .

$$\begin{array}{rl}& H_0:{\beta }_{q+1}=\cdots ={\beta }_p=0\\ & H_a:{\beta }_j\ne 0\text{ for at least one }j\end{array}$$

Drop-in-deviance test

$$\begin{array}{rl}& H_0:{\beta }_{q+1}=\cdots ={\beta }_p=0\\ & H_a:{\beta }_j\ne 0\text{ for at least one }j\end{array}$$

. . .

The test statistic is

$$\begin{array}{rl}G=D_{reduced}-D_{full}& =(-2\log L_{reduced})-(-2\log L_{full})\\ & =-2(\log L_{reduced}-\log L_{full})\end{array}$$

. . .

The p-value is calculated using a ${\chi }_{\mathrm{\Delta }df}^2$ distribution, where $\mathrm{\Delta }df$ is the number of parameters being tested (the difference in number of parameters between the full and reduced model).⁴

Example: Include education?

Should we include education in the model?

• Reduced model: age, totChol, currentSmoker

• Full model: age, totChol, currentSmoker , education

. . .

$$\begin{array}{rl}& H_0:{\beta }_{ed2}={\beta }_{ed3}={\beta }_{ed4}=0\\ & H_a:{\beta }_j\ne 0\text{ for at least one }j\end{array}$$

Example: Include education?

reduced_model <- glm(high_risk ~ age + totChol + currentSmoker, 
              data = heart_disease, family = "binomial")

full_model <- glm(high_risk ~ age + totChol + currentSmoker + education, 
              data = heart_disease, family = "binomial")

. . .

Calculate deviances

(deviance_reduced <- -2 * glance(reduced_model)$logLik)

[1] 3224.812

(deviance_full <- -2 * glance(full_model)$logLik)

[1] 3217.6

. . .

Calculate test statistic

(G <- deviance_reduced - deviance_full)

[1] 7.212113

Example: Include education?

Calculate p-value

pchisq(G, df = 3, lower.tail = FALSE)

[1] 0.06543567

. . .

What is your conclusion? Would you include education in the model that already has age, totChol, currentSmoker?

Drop-in-deviance test in R

Conduct the drop-in-deviance test using the anova() function in R with option test = "Chisq"

anova(reduced_model, full_model, test = "Chisq") |> 
  tidy() |> 
  kable(digits = 3)

term	df.residual	residual.deviance	df	deviance	p.value
high_risk ~ age + totChol + currentSmoker	4082	3224.812	NA	NA	NA
high_risk ~ age + totChol + currentSmoker + education	4079	3217.600	3	7.212	0.065

Add interactions with currentSmoker?

term	df.residual	residual.deviance	df	deviance	p.value
high_risk ~ age + totChol + currentSmoker	4082	3224.812	NA	NA	NA
high_risk ~ age + totChol + currentSmoker + currentSmoker * age + currentSmoker * totChol	4080	3222.377	2	2.435	0.296

Test for a single coefficient

Distribution of $\hat{\mathit{\beta }}$

When $n$ is large, $\hat{\mathit{\beta }}$, the estimated coefficients of the logistic regression model, is approximately normal.

How do we know the distribution of $\hat{\mathit{\beta }}$ is normal for large $n$?

Distribution of $\hat{\mathit{\beta }}$

When $n$ is large…

The expected value of $\hat{\mathit{\beta }}$ is the true parameter, $\mathit{\beta }$, i.e., $E(\hat{\mathit{\beta }})=\mathit{\beta }$

. . .

$Var(\hat{\mathit{\beta }})$, the matrix of variances and covariances between estimators

$$Var(\hat{\mathit{\beta }})=({\mathbf{X}}^{\mathsf{T}}\mathbf{V}\mathbf{X}{)}^{-1}$$

where $\mathbf{V}$ is a $n\times n$ diagonal matrix, such that $V_{ii}$ is the estimated variance for the $i^{th}$ observation

Test for a single coefficient

Hypotheses: $H_0:{\beta }_j=0\text{ vs }{H}_a:{\beta }_j\ne 0$, given the other variables in the model

. . .

(Wald) Test Statistic: $$z=\frac{{\hat{\beta }}_j-0}{SE({\hat{\beta }}_j)}$$

where $SE({\hat{\beta }}_j)$ is the square root of the $j^{th}$ diagonal element of $Var(\hat{\mathit{\beta }})$

. . .

P-value: $P(|Z|>|z|)$, where $Z\sim N(0,1)$, the Standard Normal distribution

Confidence interval for ${\beta }_j$

We can calculate the C% confidence interval for ${\beta }_j$ as the following:

$${\hat{\beta }}_j\pm z^{\ast }\times SE({\hat{\beta }}_j)$$

where $z^{\ast }$ is calculated from the $N(0,1)$ distribution

. . .

Note

This is an interval for the change in the log-odds for every one unit increase in $x_j$

Interpretation in terms of the odds

The change in odds for every one unit increase in $x_j$.

$$\exp \{{\hat{\beta }}_j\pm z^{\ast }\times SE({\hat{\beta }}_j)\}$$

. . .

Interpretation: We are $C\mathrm{\%}$ confident that for every one unit increase in $x_j$, the odds multiply by a factor of $\exp \{{\hat{\beta }}_j-z^{\ast }\times SE({\hat{\beta }}_j)\}$ to $\exp \{{\hat{\beta }}_j+z^{\ast }\times SE({\hat{\beta }}_j)\}$, holding all else constant.

Coefficient for age

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-6.673	0.378	-17.647	0.000	-7.423	-5.940
age	0.082	0.006	14.344	0.000	0.071	0.094
totChol	0.002	0.001	1.940	0.052	0.000	0.004
currentSmoker1	0.443	0.094	4.733	0.000	0.260	0.627

. . .

Hypotheses:

$$H_0:{\beta }_{age}=0\text{ vs }{H}_a:{\beta }_{age}\ne 0$$, given total cholesterol and smoking status are in the model.

Coefficient for age

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-6.673	0.378	-17.647	0.000	-7.423	-5.940
age	0.082	0.006	14.344	0.000	0.071	0.094
totChol	0.002	0.001	1.940	0.052	0.000	0.004
currentSmoker1	0.443	0.094	4.733	0.000	0.260	0.627

Test statistic:

$$z=\frac{0.0825-0}{0.00575}=14.34$$

Coefficient for age

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-6.673	0.378	-17.647	0.000	-7.423	-5.940
age	0.082	0.006	14.344	0.000	0.071	0.094
totChol	0.002	0.001	1.940	0.052	0.000	0.004
currentSmoker1	0.443	0.094	4.733	0.000	0.260	0.627

P-value:

$$P(|Z|>|14.34|)\approx 0$$

. . .

2 * pnorm(14.34,lower.tail = FALSE)

[1] 1.230554e-46

Coefficient for age

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-6.673	0.378	-17.647	0.000	-7.423	-5.940
age	0.082	0.006	14.344	0.000	0.071	0.094
totChol	0.002	0.001	1.940	0.052	0.000	0.004
currentSmoker1	0.443	0.094	4.733	0.000	0.260	0.627

Conclusion:

The p-value is very small, so we reject $H_0$. The data provide sufficient evidence that age is a statistically significant predictor of whether someone is high risk of having heart disease, after accounting for total cholesterol and smoking status.

CI for age

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-6.673	0.378	-17.647	0.000	-7.423	-5.940
age	0.082	0.006	14.344	0.000	0.071	0.094
totChol	0.002	0.001	1.940	0.052	0.000	0.004
currentSmoker1	0.443	0.094	4.733	0.000	0.260	0.627

Interpret the 95% confidence interval for age in terms of the odds of being high risk for heart disease.

Overview of testing coefficients

Test a single coefficient

• Drop-in-deviance test

• Wald hypothesis test and confidence interval

. . .

Test a subset of coefficients

• Drop-in-deviance test

. . .

Can use AIC and BIC to compare models in both scenarios

Questions from this week’s content?

Recap

• Introduced test of significance for a subset of predictors

• Inference for a single predictor

References

Wilks, SS. 1935. “The Likelihood Test of Independence in Contingency Tables.” The Annals of Mathematical Statistics 6 (4): 190–96.

Footnotes

1. See Wilks (1935) for theoretical underpinnings

2. Based on Wilk’s Theorem (Wilks 1935)

3. Example from Introduction to Statistical Learning

4. Based on Wilk’s Theorem (Wilks 1935)