Multiple linear regression

Types of predictors

Announcements

• Lab 02 due TODAY at 11:59pm

• HW 01 due Thursday, January 30 at 11:59pm

Topics

• Categorical predictors

• Centering quantitative predictors

• Standardizing quantitative predictors

• Interaction terms

Computing setup

# load packages
library(tidyverse)
library(tidymodels)
library(openintro)
library(patchwork)
library(knitr)
library(kableExtra)
library(viridis) #adjust color palette

# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_minimal(base_size = 16))

Data: Peer-to-peer lender

Today’s data is a sample of 50 loans made through a peer-to-peer lending club. The data is in the loan50 data frame in the openintro R package.

# A tibble: 50 × 4
   annual_income_th debt_to_income verified_income interest_rate
              <dbl>          <dbl> <fct>                   <dbl>
 1             59           0.558  Not Verified            10.9 
 2             60           1.31   Not Verified             9.92
 3             75           1.06   Verified                26.3 
 4             75           0.574  Not Verified             9.92
 5            254           0.238  Not Verified             9.43
 6             67           1.08   Source Verified          9.92
 7             28.8         0.0997 Source Verified         17.1 
 8             80           0.351  Not Verified             6.08
 9             34           0.698  Not Verified             7.97
10             80           0.167  Source Verified         12.6 
# ℹ 40 more rows

Variables

Predictors:

• annual_income_th: Annual income (in $1000s)
• debt_to_income: Debt-to-income ratio, i.e. the percentage of a borrower’s total debt divided by their total income
• verified_income: Whether borrower’s income source and amount have been verified (Not Verified, Source Verified, Verified)

Response: interest_rate: Interest rate for the loan

Response vs. predictors

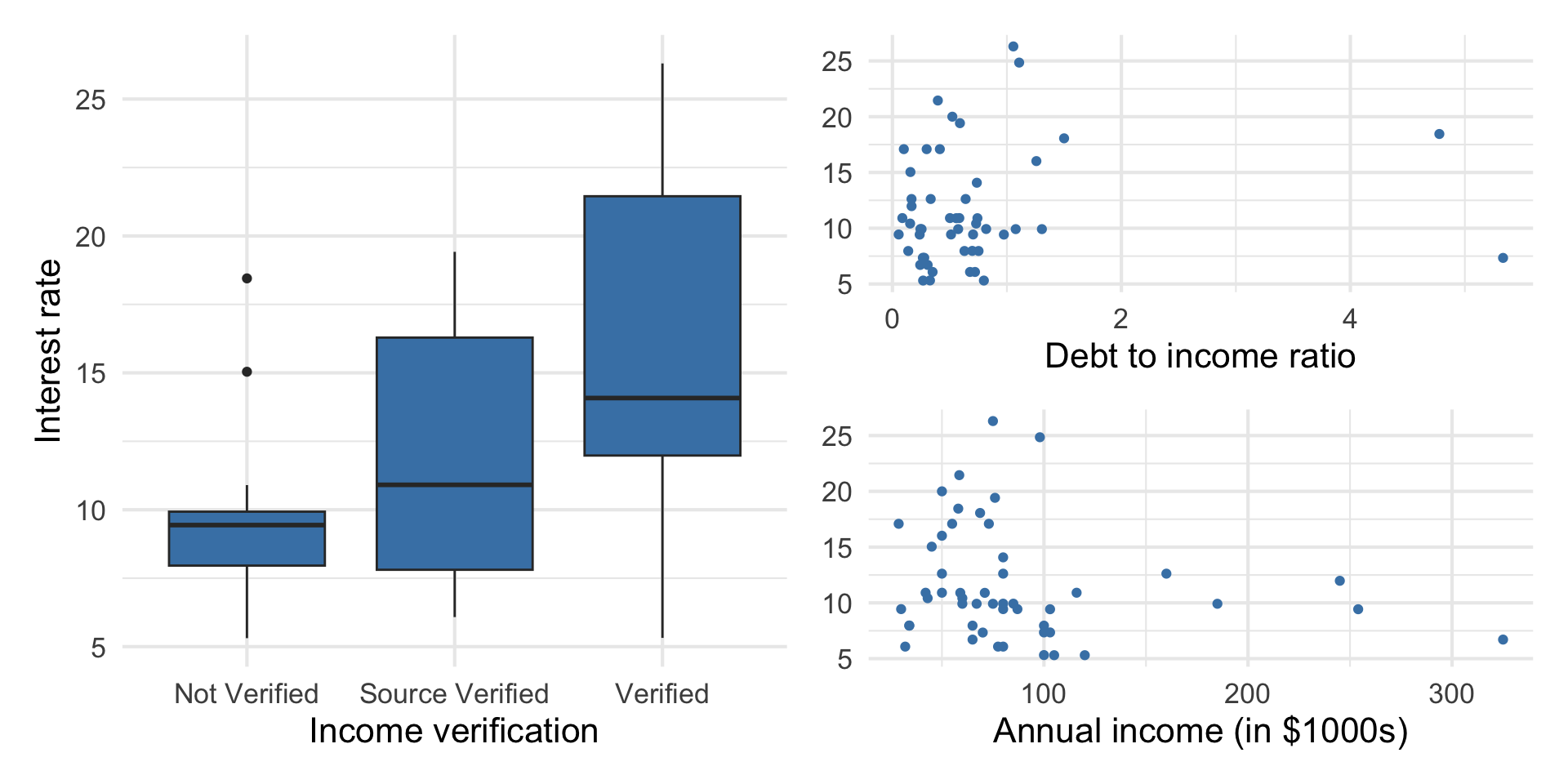
Goal: Use these predictors in a single model to understand variability in interest rate.

Model fit in R

int_fit <- lm(interest_rate ~ debt_to_income + verified_income  + annual_income_th,
              data = loan50)

tidy(int_fit) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	10.726	1.507	7.116	0.000
debt_to_income	0.671	0.676	0.993	0.326
verified_incomeSource Verified	2.211	1.399	1.581	0.121
verified_incomeVerified	6.880	1.801	3.820	0.000
annual_income_th	-0.021	0.011	-1.804	0.078

Categorical predictors

Matrix form of multiple linear regression

$$\underset{\mathbf{y}}{\underbrace{\left[\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right]}}=\underset{\mathbf{X}}{\underbrace{\left[\begin{array}{cccc}1& x_{11}& \dots & x_{1p}\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_{n1}& \dots & x_{np}\end{array}\right]}}\underset{\mathit{\beta }}{\underbrace{\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right]}}+\underset{\mathit{ϵ}}{\underbrace{\left[\begin{array}{c}{ϵ}_1\\ ⋮\\ {ϵ}_n\end{array}\right]}}$$

How might we include a categorical predictor with $k$ levels in the design matrix, $\mathbf{X}$ ?

Indicator variables

• Suppose there is a categorical variable with $k$ levels

• We can make $k$ indicator variables from the data - one indicator for each level

• An indicator (dummy) variable takes values 1 or 0

  • 1 if the observation belongs to that level

  • 0 if the observation does not belong to that level

Indicator variables

Suppose we want to predict the amount of sleep a Duke student gets based on whether they are in Pratt (Pratt Yes/ No are the only two options). Consider the model

$$Slee{p}_i={\beta }_0+{\beta }_1\mathbf{1}(Prat{t}_i=\mathtt{\text{Yes}})+{\beta }_2\mathbf{1}(Prat{t}_i=\mathtt{\text{No}})$$

• Write out the design matrix for this hypothesized linear model.

• Demonstrate that the design matrix is not of full column rank (that is, affirmatively provide one of the columns in terms of the others).

• Use this intuition to explain why when we include categorical predictors, we cannot include both indicators for every level of the variable and an intercept.

Indicator variables for verified_income

loan50 <- loan50 |>
  mutate(
    not_verified = factor(if_else(verified_income == "Not Verified", 1, 0)),
    source_verified = factor(if_else(verified_income == "Source Verified", 1, 0)),
    verified = factor(if_else(verified_income == "Verified", 1, 0))
  )

. . .

# A tibble: 3 × 4
  verified_income not_verified source_verified verified
  <fct>           <fct>        <fct>           <fct>   
1 Not Verified    1            0               0       
2 Verified        0            0               1       
3 Source Verified 0            1               0       

Indicator variables in the model

Given a categorical predictor with $k$ levels…

• Use $k-1$ indicator variables in the model
• The baseline is the category that doesn’t have a term in the model
  • This is also called the reference level
• The coefficients of the indicator variables in the model are interpreted as the expected change in the response compared to the baseline, holding all other variables constant.

Application exercise

📋 https://sta221-sp25.netlify.app/ae/ae-02-mlr.html

Complete Part 1

Interpreting verified_income

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	10.726	1.507	7.116	0.000	7.690	13.762
debt_to_income	0.671	0.676	0.993	0.326	-0.690	2.033
verified_incomeSource Verified	2.211	1.399	1.581	0.121	-0.606	5.028
verified_incomeVerified	6.880	1.801	3.820	0.000	3.253	10.508
annual_income_th	-0.021	0.011	-1.804	0.078	-0.043	0.002

. . .

• The baseline level is Not verified.
• People with source verified income are expected to take a loan with an interest rate that is 2.211% higher, on average, than the rate on loans to those whose income is not verified, holding all else constant.

Centering

• Centering a quantitative predictor means shifting every value by some constant $C$

• One common type of centering is mean-centering, in which every value of a predictor is shifted by its mean

• Only quantitative predictors are centered

• Center all quantitative predictors in the model for ease of interpretation

What is one reason one might want to center the quantitative predictors? What is are the units of centered variables?

Centering

Use the scale() function with center = TRUE and scale = FALSE to mean-center variables

loan50 <- loan50 |>
  mutate(debt_to_inc_cent = scale(debt_to_income, center = TRUE, scale = FALSE), 
         annual_inc_cent = scale(annual_income_th, center = TRUE, scale = FALSE))

lm(interest_rate ~ debt_to_inc_cent + verified_income + annual_inc_cent, data = loan50) |> 
  tidy() |> kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	9.444	0.977	9.663	0.000
debt_to_inc_cent	0.671	0.676	0.993	0.326
verified_incomeSource Verified	2.211	1.399	1.581	0.121
verified_incomeVerified	6.880	1.801	3.820	0.000
annual_inc_cent	-0.021	0.011	-1.804	0.078

Centering

Term	Original Model	Centered Model
(Intercept)	10.726	9.444
debt_to_income	0.671	0.671
verified_incomeSource Verified	2.211	2.211
verified_incomeVerified	6.880	6.880
annual_income_th	-0.021	-0.021

How has the model changed? How has the model remained the same?

Standardizing

• Standardizing a quantitative predictor mean shifting every value by the mean and dividing by the standard deviation of that variable

• Only quantitative predictors are standardized

• Standardize all quantitative predictors in the model for ease of interpretation

What is one reason one might want to standardize the quantitative predictors? What is are the units of standardized variables?

Standardizing

Use the scale() function with center = TRUE and scale = TRUE to standardized variables

loan50 <- loan50 |>
  mutate(debt_to_inc_std = scale(debt_to_income, center = TRUE, scale = TRUE), 
         annual_inc_std = scale(annual_income_th, center = TRUE, scale = TRUE))

lm(interest_rate ~ debt_to_inc_std + verified_income + annual_inc_std, data = loan50) |>
  tidy() |> kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	9.444	0.977	9.663	0.000
debt_to_inc_std	0.643	0.648	0.993	0.326
verified_incomeSource Verified	2.211	1.399	1.581	0.121
verified_incomeVerified	6.880	1.801	3.820	0.000
annual_inc_std	-1.180	0.654	-1.804	0.078

Standardizing

Term	Original Model	Standardized Model
(Intercept)	10.726	9.444
debt_to_income	0.671	0.643
verified_incomeSource Verified	2.211	2.211
verified_incomeVerified	6.880	6.880
annual_income_th	-0.021	-1.180

How has the model changed? How has the model remained the same?

Interaction terms

Interaction terms

• Sometimes the relationship between a predictor variable and the response depends on the value of another predictor variable.
• This is an interaction effect.
• To account for this, we can include interaction terms in the model.

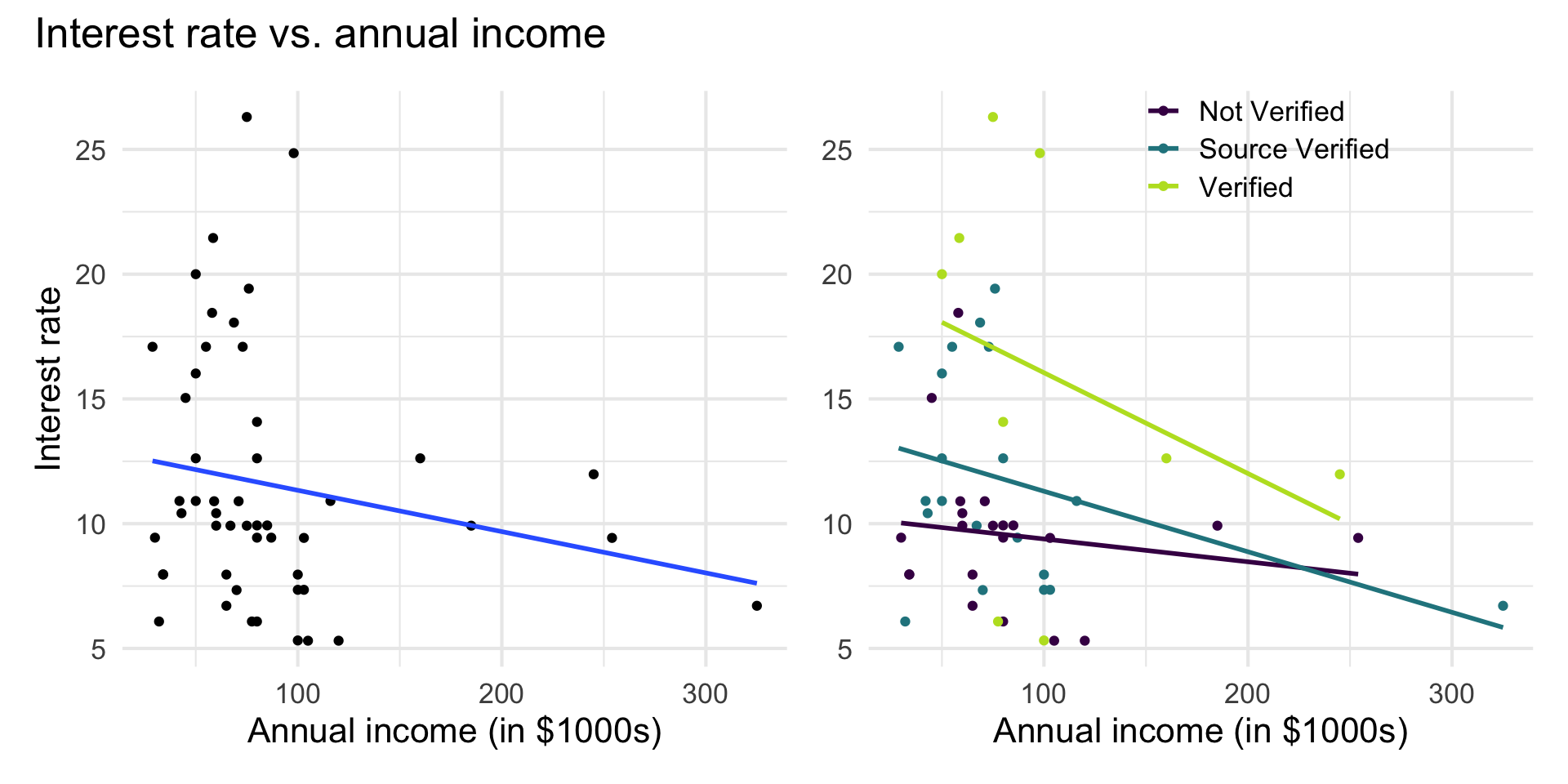
Interest rate vs. annual income

The lines are not parallel indicating there is a potential interaction effect. The slope of annual income differs based on the income verification.

Application exercise

📋 https://sta221-sp25.netlify.app/ae/ae-02-mlr.html

Complete Part 2

Interaction term in model

int_fit_2 <- lm(interest_rate ~ debt_to_income + verified_income + annual_income_th + verified_income * annual_income_th,
      data = loan50)

term	estimate	std.error	statistic	p.value
(Intercept)	9.560	2.034	4.700	0.000
debt_to_income	0.691	0.685	1.009	0.319
verified_incomeSource Verified	3.577	2.539	1.409	0.166
verified_incomeVerified	9.923	3.654	2.716	0.009
annual_income_th	-0.007	0.020	-0.341	0.735
verified_incomeSource Verified:annual_income_th	-0.016	0.026	-0.643	0.523
verified_incomeVerified:annual_income_th	-0.032	0.033	-0.979	0.333

Interpreting interaction terms

• What the interaction means: The effect of annual income on the interest rate differs by -0.016 when the income is source verified compared to when it is not verified, holding all else constant.
• Interpreting annual_income for source verified: If the income is source verified, we expect the interest rate to decrease by 0.023% (-0.007 + -0.016) for each additional thousand dollars in annual income, holding all else constant.

Recap

• Interpreted categorical predictors

• Explored by $k-1$ indicators are included in a model

• Fit and interpreted models with centered and standardized variables

• Interpreted interaction terms

Next class

• Model comparison for multiple linear regression